引言

二分搜索算法，作为一种基础且极为重要的算法策略，广泛应用于诸多领域。无论是在大规模数据的搜索与处理中，还是在数值计算的优化求解过程里，它都能展现出令人惊叹的效率。其核心思想基于对问题空间的巧妙划分与逐步逼近，通过不断将搜索范围减半，以指数级的速度收敛到目标解。这种独特的思维方式不仅为我们提供了一种高效的问题解决手段，更在算法设计的方法论层面给予我们深刻的启示。

无论是否系统地学习过二分算法，二分算法的基本思想，应该根植于每位程序员的思路中。本人在刚学习写代码的时候，如果运行的结果跟预期不一致，就会在代码近似一半的位置增加输出，先确认运行到一半时，各种中间变量的结果是否符合预期，如果此时不符合预期，就按照这个思路继续在前半代码的中间位置增加输出，否则，就在后半代码的中间位置增加输出，直到定位到问题。这种方法，不自觉使用到了二分的思想，可能可以称为：二分debug[手动狗头]

二分算法基础

让我们从一个常见的搜索问题开始理解二分算法：在一个有序数组中查找特定元素。假设我们有一个包含 n 个元素的有序数组 arr，我们要查找元素 target。

二分算法的思路是，首先确定整个数组的搜索范围，即左边界 left = 0 和右边界 right = n - 1。然后，在每次迭代中，计算中间元素的索引 mid = (left + right) / 2（这里的除法通常是向下取整）。接着，比较中间元素 arr [mid] 与目标元素 target 的大小关系：

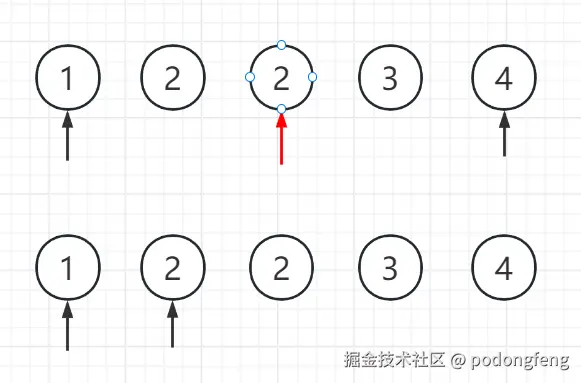
通过这样不断地将搜索区间减半，我们能够快速地逼近目标元素，大大减少了搜索的时间复杂度。

一学就会，一写就废 -- 魔鬼藏在细节中区间的定义

看了二分的基础介绍，是不是又觉得这么简单的算法，自己又行了？

那就从一道最简单的题目开始吧：leetcode-704

先看下如下的2种写法:

public int search(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + ((right - left)>>1);
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    return -1;
}

public int search(int[] nums, int target) {
    int left = 0, right = nums.length;
    while (left < right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    return -1;
}

以上2种写法不同，但都是正确的。仔细对比上述的写法后，新手可能会比较懵逼：

这其实是二分算法最重要的一个细节：边界值的处理，什么时候该用left