题目：

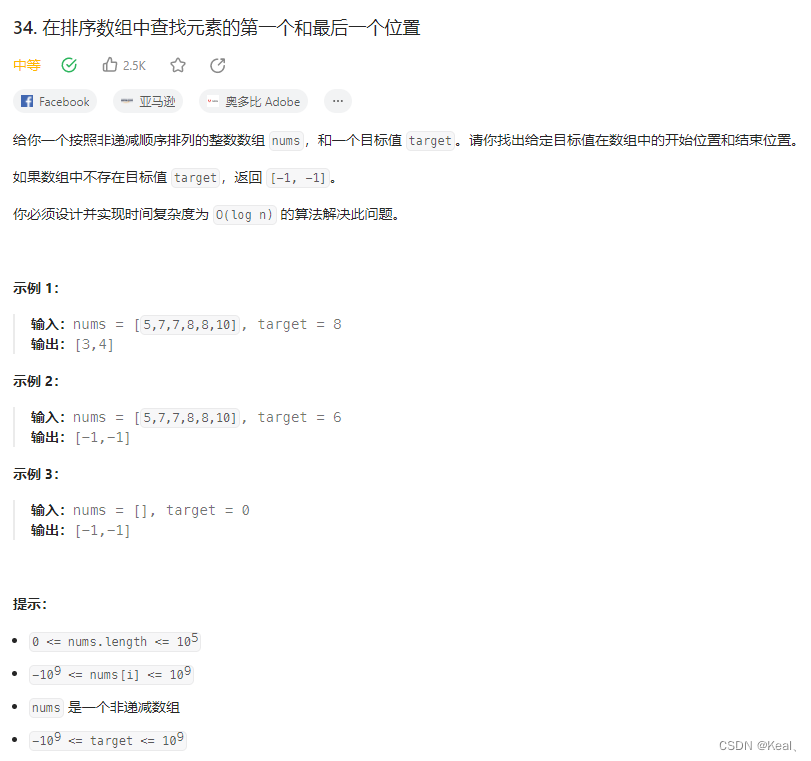
思路：

直观的思路肯定是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见的下标，但这个方法的时间复杂度为O(n)，没有利用到数组升序排列的条件。

由于数组已经排序，因此整个数组是单调递增的，我们可以利用二分法来加速查找的过程。

考虑开始和结束位置，其实我们要找的就是数组中「第一个等于的位置」和「第一个大于的位置减一」。

也相当于寻找数组中「第一个大于（ - 1）的位置」和「第一个大于的位置减一」。

最后，因为可能不存在数组中，因此我们需要重新校验我们得到的两个下标，看是否符合条件，如果符合条件就返回，看是否符合条件，如果符合条件就返回[-1,-1]。

代码：

public int[] searchRange(int[] nums, int target) {
    // 本质上找到第一个 > target - 1的作为起始，和第一个 > target的作为结束
    int start = binarySearch(nums, target - 1);
    int end = binarySearch(nums, target) - 1;
    if (end < start) {
        return new int[]{-1, -1};
    } else {
        return new int[]{start, end};
    }
}
// 注意，这里求出来的是 > mid 的第一个元素。
int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = (right + left) / 2;   // 直接找游标中间位置
        if (nums[mid] <= target) {      // 只要你等于，我就让left 往右窜一位，目的就是返回的left永远在target下一位
            left = mid + 1;
        } else {                       // 如果 >= target
            right = mid - 1;
        }
    }
    return left;
}