题目

701. 二叉搜索树中的插入操作

中等

相关标签

树二叉搜索树二叉树

给定二叉搜索树（BST）的根节点root和要插入树中的值value，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

示例 1：

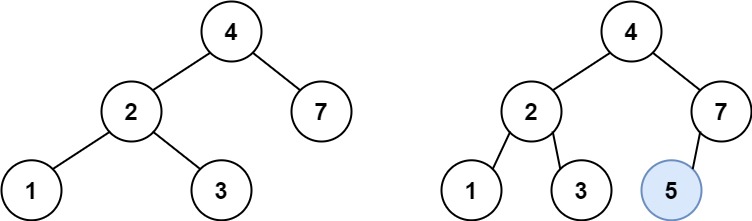
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

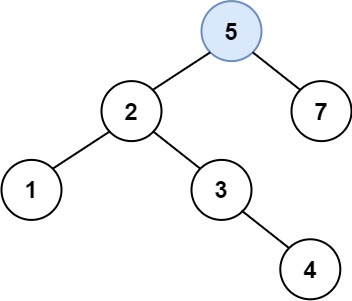
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

思路和解题方法

可以利用二叉搜索树的性质。

首先进行了一个边界情况的判断，如果当前节点为空，即找到了插入点，通过创建一个新的节点，并将新节点返回作为根节点。

如果当前节点不为空，则需要根据插入节点的值与当前节点值的大小关系，决定是往左子树还是右子树进行递归插入。

最后，返回插入节点后的根节点。

复杂度 时间复杂度:

O(log n)

时间复杂度为 O(log n)，其中 n 是二叉搜索树的节点数，因为每次插入元素都会将搜索范围缩小一半，所以时间复杂度是对数级别的。

空间复杂度

O(n)

空间复杂度取决于递归调用栈的深度，也就是二叉搜索树的高度，因为在递归过程中需要不断地压入、弹出函数栈帧，所以空间复杂度也是 O(log n)。但当树退化成链表的时候，递归调用栈的深度会达到 n，此时空间复杂度为 O(n)。

c++ 代码

class Solution {
public:
    // 向二叉搜索树中插入元素 val ，并返回插入后的根节点
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {   // 如果当前节点为空，说明找到了插入点，创建新节点，并返回
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if (root->val > val) {   // 如果插入元素比当前节点小，则往左子树中插入
            root->left = insertIntoBST(root->left, val);
        } else if (root->val < val) {  // 如果插入元素比当前节点大，则往右子树中插入
            root->right = insertIntoBST(root->right, val);
        }
        return root;  // 返回插入后的根节点
    }
};

觉得有用的话可以点点赞，支持一下。