在早期的图像分类中，通常流程是先人工提取特征，然后用对应的机器学习算法对特征进行分类，分类的准确率一般依赖特征选取的方法，甚至依赖经验主义。

Yann LeCun最早提出将卷积神经网络应用到图像识别领域的，其主要逻辑是使用卷积神经网络提取图像特征，并对图像所属类别进行预测，通过训练数据不断调整网络参数，最终形成一套能自动提取图像特征并对这些特征进行分类的网络，如图：

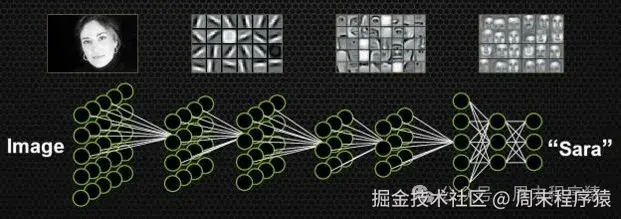
图像处理

1、卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）是一种深度学习模型，它是一种多层的神经网络，通常由输入层、卷积层（Convolutional Layer）、池化层（Pooling Layer）和全连接层（Fully Connected Layer）组成。

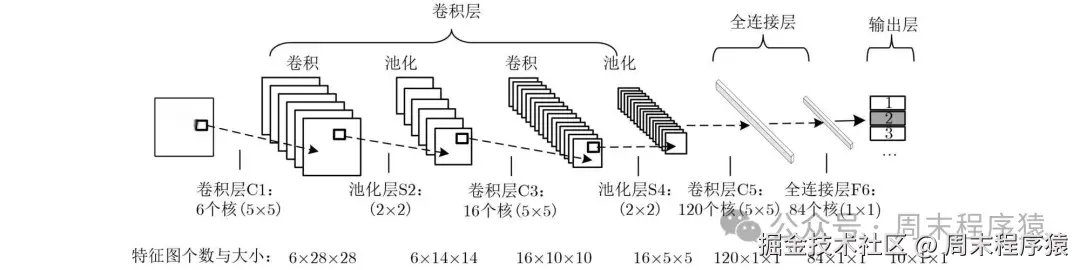
卷积神经网络

2、池化

池化在上一篇《机器学习|深度学习基础知识》介绍过，主要是降低采样率，常用的方法有平均池化，最大池化，K-均值池化等，继续上一篇代码做优化，通过pytorch的MaxPool2d函数实现最大池化：

import torch  
import torch.nn as nn  
import matplotlib.pyplot as plt  
  
# 定义包含池化层的网络  
class SimplePoolNet(nn.Module):  
    def __init__(self):  
        super(SimplePoolNet, self).__init__()  
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)  
  
    def forward(self, x):  
        return self.pool(x)  
  
# 初始化网络  
net = SimplePoolNet()  
  
# 模拟输入数据  
# 假设输入是一个1x1x4x4的张量（NxCxHxW），其中N是批次大小，C是通道数  
input_tensor = torch.tensor([[[[1, 2, 3, 4],  
                               [5, 6, 7, 8],  
                               [9, 10, 11, 12],  
                               [13, 14, 15, 16]]]])  
  
# 执行池化操作  
output_tensor = net(input_tensor)  
  
# 可视化输入和输出  
plt.figure(figsize=(10, 5))  
  
# 显示输入  
plt.subplot(1, 2, 1)  
plt.imshow(input_tensor.squeeze(0).squeeze(0), cmap='gray')  
plt.title('Input')  
  
# 显示输出  
plt.subplot(1, 2, 2)  
plt.imshow(output_tensor.squeeze(0).squeeze(0), cmap='gray')  
plt.title('Output')  
  
plt.show()

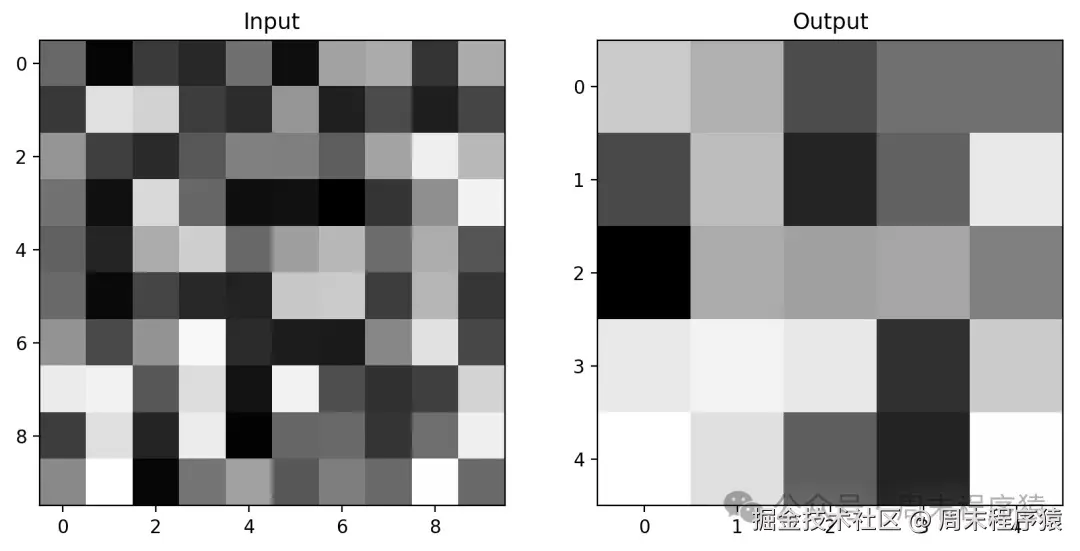
池化

从上面生成的Output可以看出，池化有如下有点：

3、卷积3.1 为什么需要卷积？

为什么需要卷积？在全连接网络中，输入层是100X100的矩阵（可以是图像，也可以是其他特性信息），会被变换为10000X1的向量，这样会存在几个问题？

为了解决这些问题，所以卷积计算就出现了，具体怎么做的呢？

import torch  
import torch.nn as nn  
  
# 随机生成一个10x10x1的矩阵（假设是单通道图像）  
input_tensor = torch.rand(1, 1, 10, 10)  # (batch_size, channels, height, width)  
  
# 定义一个3x3的卷积层，padding=1以确保输出尺寸与输入相同  
conv_layer = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1)  
  
# 初始化卷积层的权重（这里PyTorch会自动处理）   
print("Initial weights of the convolution layer:")  
print(conv_layer.weight)  
  
# 进行卷积计算  
output_tensor = conv_layer(input_tensor)  
  
# 打印输出张量的尺寸  
print("Output tensor shape:", output_tensor.shape)  
  
# 如果需要，可以打印输出张量的具体内容  
print(output_tensor)

为了方便理解，我从（poloclub.github.io/cnn-explain…

图片卷积计算过程

3.2 卷积计算

上一节说了为什么要有卷积，知道卷积就是类似滤波器做矩阵运算，其中具体过程如下：

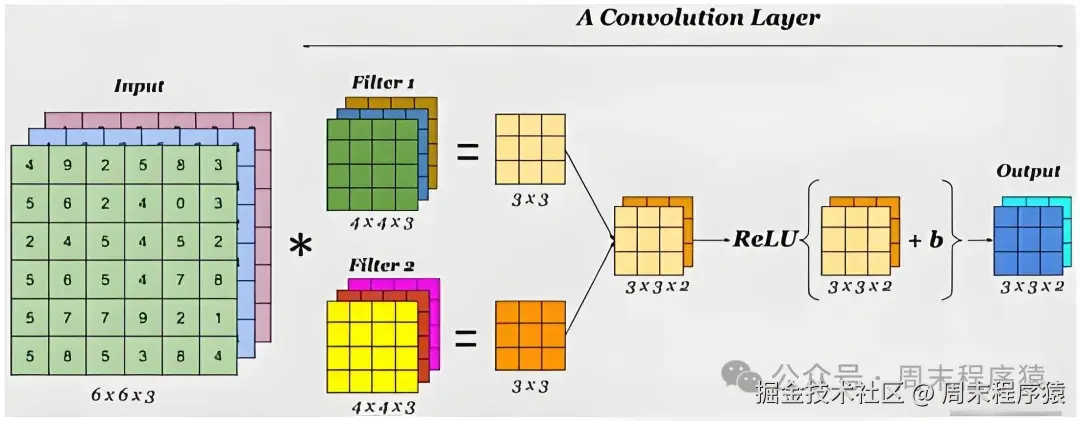
卷积计算

卷积核：卷积核是卷积运算的参数，它是一个矩阵，其数值对图像中与卷积核同样大小的子块像素点进行卷积计算时所采用的权重；

权重系数：权重系数就是卷积核的参数，捕获图像中某像素点及其邻域像素点所构成的特有空间模式；

填充：填充是指在图像边缘添加像素点，使得卷积核可以覆盖到整个图像，避免卷积运算时输入图像尺寸变小；

步长：步长是指卷积核移动的步数，一般设置为2或者1，在图像上表示移动多少个像素点，比如步长为2，图像为100X100，卷积后的矩阵就是50X50；

感受野：感受野是指卷积核覆盖的区域，比如3X3的卷积核，1层卷积感受野为3X3，2层卷积感受野为5X5...，根据最后一层卷积核与原始图像的关联关系；

多维卷积核：多维卷积核是指卷积核的维度大于2，比如3D图像的卷积核就是3X3X3；

3.3 卷积算子3.3.1 1X1卷积

1X1卷积，即输入通道数与输出通道数相同，不去考虑输入数据局部信息之间的关系，而把关注点放在不同通道间，比如输入通道数为3，输出通道数为3，那么就是对每个通道做1X1卷积，得到3个输出通道。

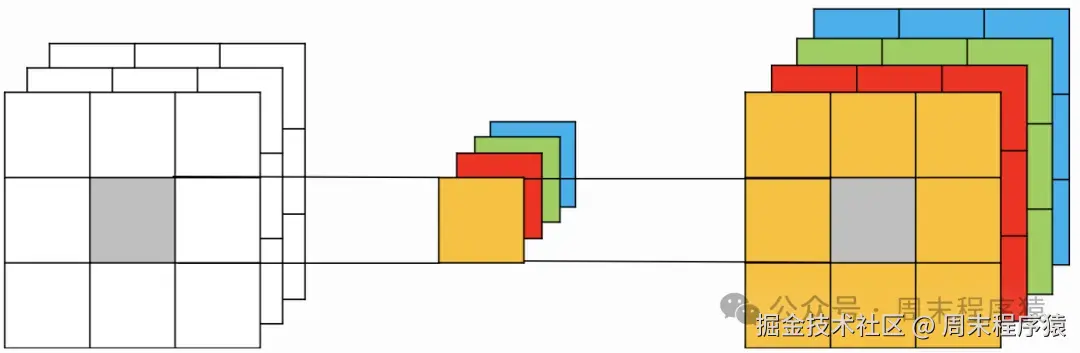
1X1卷积

从这里看，2D情况下1X1并没有特殊之处，但是高维情况下，1X1就可以实现降维或者升维的效果，比如将各个维度相同矩阵通过1X1卷积，就可以获得2D矩阵。

3.3.2 3D卷积

3D与2D卷积的区别是多了一个维度，输入由(,ℎℎ,ℎ)变为(,ℎ,ℎℎ,ℎ)，与之对应的应用场景如视频和医疗图像图片等，其中示意图和样例代码如下：

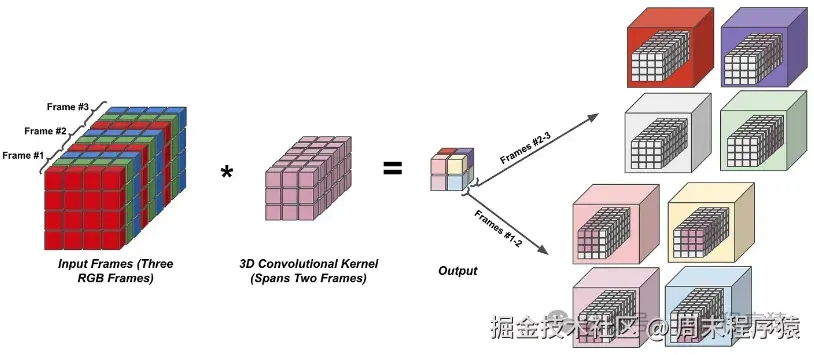
3D卷积

import torch
import torch.nn as nn
# 输入数据
# 假设我们有一个批量大小为1，具有1个通道的3D数据，其尺寸为(3, 3, 3)
input_data = torch.tensor([[
    [
        [[1, 2, 3], [4, 5, 6], [7, 8, 9]],
        [[10, 11, 12], [13, 14, 15], [16, 17, 18]],
        [[19, 20, 21], [22, 23, 24], [25, 26, 27]]
    ]
]], dtype=torch.float32)
# 定义3D卷积层
# 输入通道数为1，输出通道数为1，卷积核尺寸为(2, 2, 2)，步长为1，填充为0
conv3d_layer = nn.Conv3d(in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0)
# 初始化卷积核权重
conv3d_layer.weight.data = torch.tensor([[
    [
        [[1, 2], [3, 4]],
        [[5, 6], [7, 8]]
    ]
]], dtype=torch.float32)
# 初始化偏置
conv3d_layer.bias.data = torch.tensor([0], dtype=torch.float32)
# 计算3D卷积输出
output = conv3d_layer(input_data)
# 输出结果
print("Output shape:", output.shape)
print("Output data:", output)

3.3.3 转置卷积

什么是转置卷积？

卷积的逆运算，用于增加上采样中间层特征图的空间维度，与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出，其中示意图和样例代码如下：

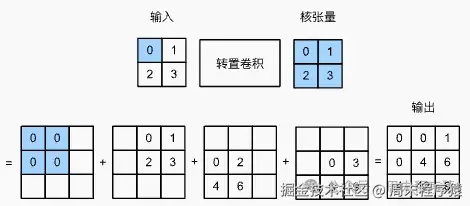
转置卷积

def trans_conv(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i: i + h, j: j + w] += X[i, j] * K
    return Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
tcov = trans_conv(X, K)
print("trans_conv: ", trans_conv)
# 输出结果
tensor([[ 0.,  0.,  1.],
        [ 0.,  4.,  6.],
        [ 4., 12.,  9.]])

3.3.4 空洞卷积

空洞卷积顾名思义就补足空洞，通过类似上采样的方式填充图片，比如：

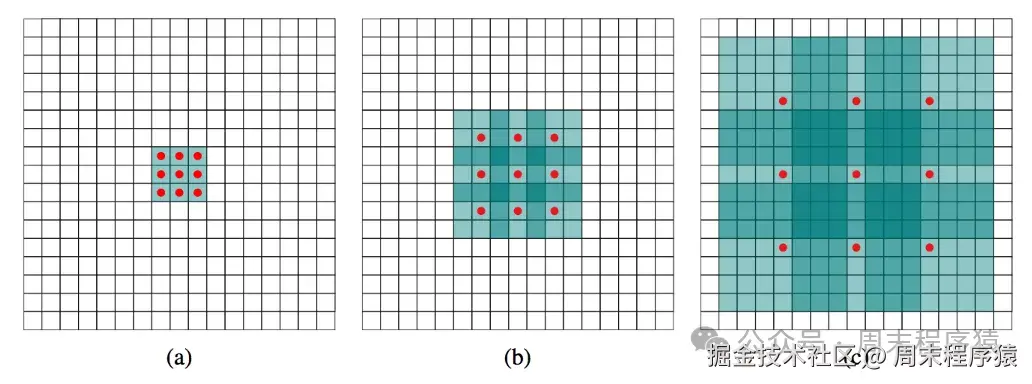
空洞卷积

3.3.5 分离卷积

卷积神经网络解决了计算机视觉领域大部分问题，但是可以看到上面一个问题，就是卷积计算是通过矩阵操作，计算量比较大，如何降低计算量呢？扩展到工业领域？利用矩阵计算的特点，将矩阵分解为两个矩阵相乘，如下图所示：

分离卷积

利用矩阵原理是拆分两个向量的外积：

卷积外积

这样可以看出计算量对比：原始的计算量为9次，而拆分计算量为3次+3次，比原始的计算量少了3次，所以对于更大的矩阵计算量将大大减少。

4、LeNet卷积神经网络

前面已经介绍卷积模型，那么看看最早的卷积神经网络是如何设计，总体看来，由两部分组成：

LeNet架构图

代码可以参考：zh.d2l.ai/chapter_con…

import torch
from torch import nn
from d2l import torch as d2l
# LeNet-5 
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)
batch_size = 256
# 下载Fashion-MNIST数据集
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
# 计算数据集上的精度
def evaluate_accuracy_gpu(net, data_iter, device=None):
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]
# 训练letnet
def train_letnet(net, train_iter, test_iter, num_epochs, lr, device):
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')
    
lr, num_epochs = 0.9, 10
train_letnet(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# 输出结果（运行在CPU上）
Conv2d output shape:     torch.Size([1, 6, 28, 28])
Sigmoid output shape:    torch.Size([1, 6, 28, 28])
AvgPool2d output shape:          torch.Size([1, 6, 14, 14])
Conv2d output shape:     torch.Size([1, 16, 10, 10])
Sigmoid output shape:    torch.Size([1, 16, 10, 10])
AvgPool2d output shape:          torch.Size([1, 16, 5, 5])
Flatten output shape:    torch.Size([1, 400])
Linear output shape:     torch.Size([1, 120])
Sigmoid output shape:    torch.Size([1, 120])
Linear output shape:     torch.Size([1, 84])
Sigmoid output shape:    torch.Size([1, 84])
Linear output shape:     torch.Size([1, 10])
...
loss 0.465, train acc 0.825, test acc 0.783
6611.0 examples/sec on cpu

参考

（1）paddlepedia.readthedocs.io/en/latest/t…

（2）zh.d2l.ai/chapter_con…