1、题目1:226-翻转二叉树

题目：/problems/in…

类型：简单

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

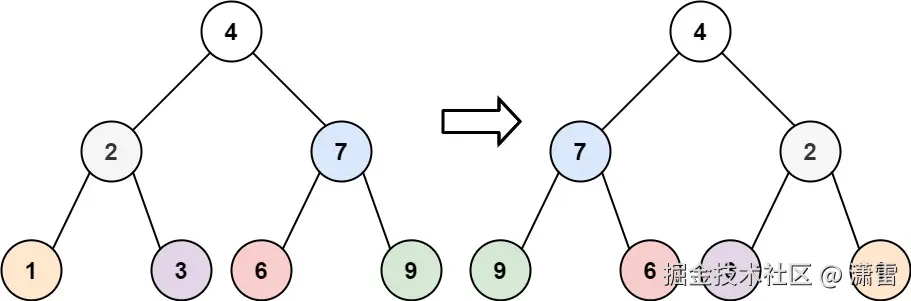
输入： root = [4,2,7,1,3,6,9] 输出： [4,7,2,9,6,3,1]

思路1：递归法

建议采用前序遍历或后续遍历。前左右。

递归写法：

public TreeNode invertTree(TreeNode root) {
    if(root == null){
        return root;
    }
    invertTree(root.left);
    invertTree(root.right);
    swapChildren(root);
    return root;
}
private void swapChildren(TreeNode root) {
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;
}

注意：本题如果要采用中序处理的话，不太建议，如果要写，就遍历两次左边，因为子树做了交换。

思路2：层序遍历法

public TreeNode invertTree2(TreeNode root){
    if(root == null){
       return null;
    }
    ArrayDeque queue = new ArrayDeque<>();
    queue.offer(root);
    while (queue.size()>0){
        int size = queue.size();
        while (size-- >0){
            TreeNode pop = queue.pop();
            swapChildren(pop);
            if(pop.left!=null){
                queue.offer(pop.left);
            }
            if(pop.right !=null){
                queue.offer(pop.right);
            }
        }
    }
    return root;
}
private void swapChildren(TreeNode root) {
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;
}

2、题目2:101-对称二叉树（递归）

题目：/problems/sy…

给定一个二叉树，检查它是否是镜像对称的。

输入： root = [1,2,2,3,4,4,3] 输出： true

判断左子树和右子树是否可以翻转，比较的是外侧的节点。

二叉树的题目确定顺序是非常重要的。我们这题目只能使用后序，因为我们要不断收集左右孩子的节点给上一个节点，将比较结果的信息返回上一层。

public class Number101_1 {
    public static void main(String[] args) {
        TreeNode treeNode = new TreeNode(1);
        TreeNode node = new TreeNode(2);
        node.left = new TreeNode(3);
        node.right = new TreeNode(4);
        TreeNode node2 = new TreeNode(2);
        node2.left = new TreeNode(4);
        node2.right = new TreeNode(4);
        treeNode.left = node;
        treeNode.right =node2;
        System.out.println(isSymmetric(treeNode));
    }
    public static boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return compareRes(root.left, root.right);
    }
    private static boolean compareRes(TreeNode left, TreeNode right) {
        //边界条件
if(left == null && right!=null) return false;
        if(left !=null && right == null) return false;
        if(left == null && right == null) return true;
        if(left.val != right.val) return false;
        // 每一层的逻辑，比较的是镜像的数据
boolean innerRes = compareRes(left.right, right.left);
        boolean outRes = compareRes(left.left, right.right);
        if(innerRes && outRes){
            return true;
        }
        return false;
    }
}

3、题目3:104-二叉树的最大深度（递归）

题目：/problems/ma…

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

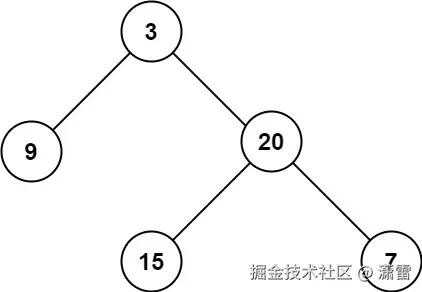
输入： root = [3,9,20,null,null,15,7] 输出： 3

思路：

先搞清楚深度和高度，

例如上面的15的高度是1，深度是3。如果求高度，是从下往上遍历，那只能用后序，如果要求深度，从上往下遍历，则采用前序。

但是因为高度和深度相等，所以给出的高度答案也是可以通过的

class Solution {
    public int maxDepth(TreeNode root) {
       if(root == null){
            return 0;
        }
        int leftHeight = maxDepth(root.left);//左
        int rightHeight = maxDepth(root.right);//右
        int hegiht = 1+ Math.max(leftHeight,rightHeight);//中
        return hegiht;
    }
}

使用层序遍历解决：用层序遍历是挺容易的。

public int maxDepth2(TreeNode root) {
    if(root == null){
        return 0;
    }
    LinkedList queue = new LinkedList<>();
    queue.offer(root);
    int height = 0;
    while (queue.size()>0){
        int size =queue.size();
        height++;
        while (size-- >0){
            TreeNode pop = queue.pop();
            if(pop.left!=null){
                queue.offer(pop.left);
            }
            if(pop.right !=null){
                queue.offer(pop.right);
            }
        }
    }
    return height;
}

4、题目4:111-二叉树的最小深度

题目：/problems/mi…

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

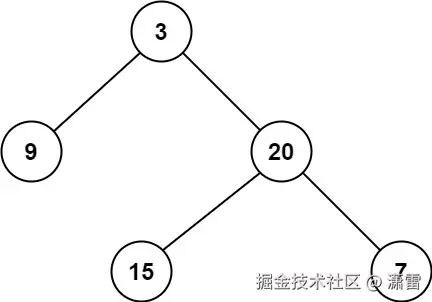
输入： root = [3,9,20,null,null,15,7] 输出： 2

思路：层序遍历我觉得很容易找到深度啥的，所以先用层序遍历试试解决。

public int minDepth(TreeNode root) {
    if(root == null){
        return 0;
    }
    LinkedList queue = new LinkedList<>();
    queue.offer(root);
    int depth = 0;
    while (queue.size()>0){
        int size =queue.size();
        depth++;
        while (size-- >0){
            TreeNode node = queue.pop();
            if(node.left == null && node.right ==null){
                return depth;
            }
            if(node.left !=null){
                queue.offer(node.left);
            }
            if(node.right !=null){
                queue.offer(node.right);
            }
        }
    }
    return depth;
}

再考虑迭代的思想，

public int minDepth2(TreeNode root) {
    if(root == null){
        return 0;
    }
    int leftDepth = minDepth(root.left);
    int rightDepth = minDepth(root.right);
    if(root.left == null){
        return rightDepth+1;
    }
    if(root.right == null){
        return leftDepth+1;
    }
    // 左右节点都不为null
return Math.min(leftDepth,rightDepth)+1;
}