前言

对于刚刚入行的前端开发者，尤其是在三维医疗图像领域工作的初学者，理解一些基础的计算机图形学概念是必不可少的。这些概念不仅帮助你理解如何操作三维空间中的对象，还会让你更好地处理与图像相关的任务。本文将围绕向量展开，介绍向量在三维图像中的作用，帮助你快速理解并应用这些数学知识。

什么是向量？

在计算机图形学中，向量是一种重要的数学工具，通常用于描述空间中的位置、方向和大小。向量在二维或三维空间中的图像处理、动画、物体移动以及物体之间的碰撞检测中都有广泛的应用。

1. 向量的基本概念

一个向量可以简单理解为具有方向和长度的量。我们用一个有序的数对或数三元组来表示向量。在三维空间中，向量用 (x, y, z) 表示，x、y 和 z 表示向量在三个不同维度上的分量。例如，向量 (3, 4, 5) 可以表示一个从原点 (0, 0, 0) 到位置 (3, 4, 5) 的方向和长度。

2. 向量的长度

向量的长度（或称作模）反映了向量的大小，表示从起点到终点的距离。在三维空间中，向量的长度可以通过以下公式计算：

length=x2+y2+z2{length} = \sqrt{x^2 + y^2 + z^2} length=x2+y2+z2​

示例：

给定向量 A = (3, 4, 0)，它的长度是：

length=32+42+02=5{length} = \sqrt{3^2 + 4^2 + 0^2} = 5 length=32+42+02​=5

长度在三维医疗图像处理中特别重要，因为它能表示物体之间的距离，或是一个物体沿某个方向移动的距离。

计算机图形学中的向量运算

在计算三维图像时，我们经常会涉及到各种向量运算，比如加法、减法、点乘和叉乘。这些运算有助于我们对三维空间中的物体进行处理和变换。

1. 向量加法和减法示例：

假设我们有两个向量 A = (3, 2, 5) 和 B = (1, 0, -2)，则：

向量的加减在图形学中用来表示物体位移或合成多个运动方向。例如，当你需要从一个位置移动到另一个位置时，你可以通过向量相加或相减计算出所需的运动路径。

2. 向量的点乘（Dot Product）

点乘是两个向量之间的运算，结果是一个标量（数值）。点乘可以帮助我们了解两个向量之间的夹角，用于计算光照、物体之间的角度等。

点乘公式：

给定两个向量 A = (x1, y1, z1) 和 B = (x2, y2, z2)，它们的点乘为：

A⋅B=x1×x2+y1×y2+z1×z2A⋅B=x1×x2+y1×y2+z1×z2 A⋅B=x1×x2+y1×y2+z1×z2

点乘的意义：示例：

对于 A = (1, 0, 0) 和 B = (0, 1, 0)：

A⋅B=1×0+0×1+0×0=0A⋅B=1×0+0×1+0×0=0 A⋅B=1×0+0×1+0×0=0

表示 A 和 B 是垂直的。

在三维医疗图像处理中，点乘经常用于光照计算，例如计算光线和物体表面法线的夹角，从而确定物体表面的明暗程度。

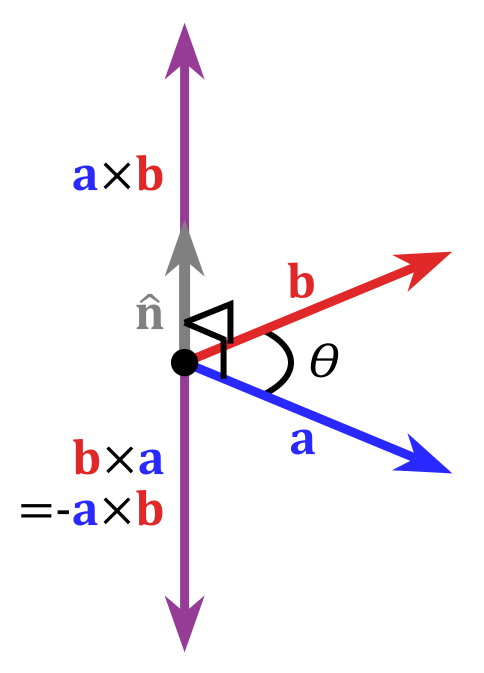
3. 向量的叉乘（Cross Product）

叉乘是两个向量运算的另一种方式，它返回一个新的向量，这个向量垂直于原来的两个向量。叉乘常用于计算三维空间中的法线向量，如表面法线，用于处理光照、碰撞检测等问题。

叉乘公式：

给定两个向量 A = (x1, y1, z1) 和 B = (x2, y2, z2)，它们的叉乘为：

A×B=(y1×z2−z1×y2,z1×x2−x1×z2,x1×y2−y1×x2)A×B=(y1×z2−z1×y2, z1×x2−x1×z2, x1×y2−y1×x2) A×B=(y1×z2−z1×y2,z1×x2−x1×z2,x1×y2−y1×x2)

示例：

对于 A = (1, 0, 0) 和 B = (0, 1, 0)，它们的叉乘结果为：

A×B=(0,0,1)A×B=(0,0,1) A×B=(0,0,1)

表示得到的向量垂直于 A 和 B。

在三维医疗图像处理中，叉乘可以用来计算物体的旋转轴，或计算图像中表面法线的方向，用于光照或着色计算。

特别应用：单位向量与方向向量1. 单位向量（Unit Vector）

单位向量是长度为1的向量，它表示纯粹的方向。单位向量广泛用于表示物体的方向或光照方向。

如何计算单位向量？

单位向量是通过将向量的每个分量除以其长度得到的。假设向量 A = (x, y, z) 的长度为 L：

UnitVector=(xL,yL,zL)\text{Unit Vector} = \left( \frac{x}{L}, \frac{y}{L}, \frac{z}{L} \right) UnitVector=(Lx​,Ly​,Lz​)

示例：

对于向量 A = (3, 4, 0)，它的单位向量为：

UnitVector=(35,45,0)=(0.6,0.8,0)\text{Unit Vector} = \left( \frac{3}{5}, \frac{4}{5}, 0 \right) = (0.6, 0.8, 0) UnitVector=(53​,54​,0)=(0.6,0.8,0)

在三维医疗图像领域，单位向量通常用于描述摄像机的朝向或光源的方向，从而影响渲染结果。

2. 方向向量（Direction Vector）

方向向量用于表示从一个点到另一个点的方向。例如，在三维空间中，如果有两个点 P1 = (x1, y1, z1) 和 P2 = (x2, y2, z2)，那么方向向量为：

DirectionVector=(x2−x1,y2−y1,z2−z1)\text{Direction Vector} = (x2 - x1, y2 - y1, z2 - z1) DirectionVector=(x2−x1,y2−y1,z2−z1)

示例：

从点 P1 = (1, 2, 3) 到 P2 = (4, 6, 9) 的方向向量是：

DirectionVector=(4−1,6−2,9−3)=(3,4,6)\text{Direction Vector} = (4 - 1, 6 - 2, 9 - 3) = (3, 4, 6) DirectionVector=(4−1,6−2,9−3)=(3,4,6)

在医疗图像处理系统中，方向向量可以用于确定图像中不同物体之间的相对位置和方向，例如计算医学影像中器官的移动方向。

结语

理解向量及其运算是进入三维医疗图像处理领域的关键一步。虽然这些数学知识可能看起来比较抽象，但它们是图形学、光照计算、碰撞检测等操作的基础。在实际项目中，随着对三维图像处理的深入，你会发现这些基础向量运算为你提供了强大的工具，使得复杂的三维场景变得更加可控和可操作。

希望这篇文章能够帮助你快速了解计算机图形学中的向量相关知识，让你在三维医疗图像领域的前端开发之路上走得更加顺利。